WBSSC SLST Math Syllabus 2025 [LATEST] Download PDF: West Bengal SSC 2nd SLST New Mathematics Syllabus 2025 for Assistant Teacher Recruitment Exam is given here. Math Syllabus for Class 9, 10 Graduate Teacher and Class 11, 12 PG Teacher can be downloaded from the links below in PDF format. The syllabus has been taken from 1st SLST 2016 & Santhali Medium School Teacher Recruitment Syllabus 2019-21.
Important Links
| SLST Mathematics ক্লাস ৯ , ১০ এর সিলেবাস (Graduate Teacher) | Download |
| SLST Mathematics ক্লাস ১১ , ১২ এর সিলেবাস (PG Teacher) | Download |
| Facebook Group for 2nd SLST Preparation 2025 | Join Now |
| SLST 2025 Notification | Click Here |
| SLST Syllabus {All Subject} | Click Here |
| SLST Previous Question Paper {All Subject} | Click Here |
West Bengal SSC SLST Math Syllabus for Class 9, 10










SLST Mathematics Syllabus for Class 11, 12
CLASSICAL ALGEBRA:
- Integers: Statement of well ordering Principle, first and second principles of mathematical induction. Proofs of some simple mathematical results by induction. Divisibility of integers. The division algorithm. The greatest common divisor of two integers a and b – its existence and uniqueness. Relatively prime integers. Prime integers. Euclid’s first theorem; if some prime p divides ab, them p divides a or b. Euclid’s second theorem: there are infinitely many prime integers. Unique factorization theorem.
- Complex numbers: Definition on the basis of ordered paris. Algebra of complex numbers, Modulus, Amplitudes, Argand Diagram, De-Moivre’s theorem and its applications, Exponential, Sine, Cosine and Logarithm of a complex number.
Definition of az ( a ≠ 0), Inverse Circular and Hyperbolic functions. - Polynomials with real co-efficeints: Fundamental theorem of classical algebra (statement only). The nth degree Polynomial equation has exactly n roots. Nature of roots of an equation (Surd and imaginary) roots occur in pairs). Statement of Decartes rule of signs and its applications. Multiple roots. Relation between roots and coefficients. Symmetric functions of roots. Transformation of equations. Reciprocal equations. Cardan’s method of solving a cubic equation. Ferrari’s method of solving a bi-quadratic equation.
- Inequalities: A. M. ≥ G.M. ≥ H.M. and Cauchy’s inequality – their simple and direct applications.
MODERN ALGEBRA:
- Basic Concepts: Sets, subsets, equality of sets, operations on sets – Union, Intersection, Complements and Symmetric difference. Properties including De-Morgan’s laws. Cartesian products, Binary relation from a set to a set (domain, range, Examples from R x R). Equivalence relation. Fundamental thereon on Equivalence relation. Partition, Relation of partial order. Congruence relation modulo n is an equivalence relation.. Congruence classes. Mapping Inijection, Surjection and Bijection. Inverse and Identity mapping. Composition of mappings and its associativity.
- Introduction of Group Theory: Groupoid, Semi-group, Monoid, Group definition with both sided identity and inverses. Examples of finite and infinite groups taken from various branches. Additive (multiplicative) group of integers modulo an integer (resp. a prime). Klein’s 4 group Integral powers of an element and laws of indices in a group. Order a group and order of an element of a group. Subgroups. Nec. And Suff. Condition for a subset of a group to be subgroup. Intersection and Union of two subgroups. Cosets and Lgrange’s theorem. Cyclic groups – definition, examples and subgroups of cyclic groups. Generators Permutations. Cycle. Transposition. Even odd permutations. Symmetric group. Definition and order of Alternating subgroup. Normal subgroups of a group — Definition, examples and characterizations.
Quotient group of a group by a normal subgroup. Homomorphism and Isomorphism of groups. Kernel of homomorphism. Fundamental theorem of homomorphism. An infinite cyclic group is isomorphic to (z, +) and a finite cyclic group of order n is isomorphic to the group or residue classes modulo n. - Introduction to rigns and fields: Ring-definition and example. Ring of integers modulo n. Properties directly following from the definition. Integral domain and Field-Definitions and examples. Sub-ring sub-field & characteristic of a ring.
MATRIX THEORY AND LINEAR ALGEBRA:
- Matrices of Real and Complex Numbers: Definition, examples, equality, addition, multiplication of matrices, Transpose of a matrix, Symmetric and Skew-symmetric matrices.
- Determinants: Definition of a determinant of a square matrix, Basic properties, Minors and Cofactors, equations by Cramer’s rule. Problems of determinants up to order 3.
- Rank of a Matrix: Adjoint of a square matrix. For a square matrix A of order n, A. Adj. A – Adj A. A = det A. Singular, non-singular and invertible matrices. Elementary operations. Rank of matrix and its determination. Normal forms: Elementary matrices; The normal form equivalence of matrices. Congruence of Matrices. Diagonalisation of matrices. Real quadratic from involving three variable. Reduction to Normal form.
- Vector/ Linear Space Over a Field: Definition and example of vector space. Subspace. Union, Intersection and sum of vector spaces. Linear span. Generators and basis of a vector spaces. Formation of basis from linearly independent subset. Special emphasis of R.
- Row-space and column-space of a matrix: Definitions of row-space and column-space of a matrix. Row rank, column rank and Rank of a matrix.
- System of Linear Equations: Solution space of a homogeneous system as a subspace. Condition for the existence of non-trivial solution of a system of linear homogeneous equations. Necessary and sufficient conditions for the consistency of a system of non-homogeneous equations. Solution of system of equations by matrix method.
- Linear Transformation on Vector Spaces: Definition of linear transformation. Null space, Range space, Rank and Nullity of linear transformation. Sylvester’s law of Nullity. (Inverse of linear transformation relative to ordered bases of finite dimensional vector spaces.)
- Inner product space: Definition and examples. Norm. Euclidean Vector space – Triangle inequality and Cauchy – Schwarz inequality in Euclidean vector space. Orthogonality of vectors. Orthonormal basis. Gram-Schmidt process of Orthonormalization.
- Eigen value and Eigen vector, Characteristics equation of a square matrix. Caley-Hamilton’s Theorem. Simple properties of Eigen values and Eigen vectors.
- Real-Number: Geometric representation and Cantor, Dedekind Axiom. Salient properties taken as axioms Bounded set. Least upper bound axioms. Archimedean property. Decimal representation of real numbers.
- Points Sets in R1 and R2: Elementary properties and union of atmost denumerable sets. Denumberability of rational numbers and non-denumberability of real numbers and of an interval. Neighbourhood of a point, interior point, of linear point set, open and closed sets, limit point of a set in R1 and R2 concepts and simple properties. Union, intersection and complement of open and closed sets and Bolzano-Weiestrass theorem in R1. Covering by open intervals of linear point set, Lindeloff covering theorem and Heine Borel theorem (statements only) and compact sets in R1.
- Real-valued functions defined on intervals: Bounded and monotonic functions. Limits, Algebra of limits. Sandwich rule, condition for the existence of a finite limit. Important limits like.
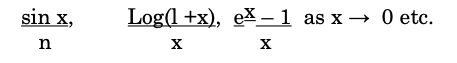
4. Infinite Series of Constant Terms: Convergene and divergene. Cauchy’s criterion. Abel-Pringsheim’s Test. Tests (Comparison test, Root Test) convergence of series of non-negative terms.
5. Series of arbitrary terms. Absolutely convergent and conditionally convergent series. Alternative series. Leibnitz test. Root and Ratio Tests. Non-absolute convergence — Abel’s and Dirichlet’s tests (statement and applications)
6. Continuity of a function at a point and on an interval: Continuity of some standard functions, continuity of composite functions. Piecewise continuous functions. Uniform continuity. Discontinuities of different kinds. Properties of continuous functions on a closed interval. Existence of inverse functions of a strictly monotone function and its continuity.
7. Concept of Differentiability and differential: Chain rule. Sign of derivative. Successive derivatives. Leibnitz theorem. Theorms on Derivatives : Darbox theorem, Rolle’s theorem. Mean value theorems of Lagrange and Cauchy. Taylor’s theorem.
Maclaurin’s series. Expansion of ex, ax, a > 0, log (l+x) (l+x)m, Sinx, Cosx etc. with their respective ranges of validity.
8. Indeterminate forms: L Hospital’s rule and its consequences.
9. Maxima and Minima: Points of local extremum of a functions in an interval. Sufficient condition for the existence of a local miximum/minimum of a function at a point. Applications in Geometrical and Physical problems.
10. Tangents and Normals: Pedal equation, Peadal of a curve, Rectilinear Asympotes (Cartesian and parametric form). Curvature- radius and centre of curvature. Chord of curvature. Curve-Tracing (familiarity with well-known curves)

Area enclosed by a curve, length of a curve.
Sequence of functions: Pointwise and uniform convergence. Cauchy’s criterion of uniform convergence. Limit function:
Boundness, Repeated limits, continuity and differentiability.
Series of functions: Pointwise and uniform convergence. Tests of convergence statements of Abel’s and Dirichlet’s tests and their applications.
Passage to the limit term-by-term; boundedness, continuity, integrability and differentiability of a series of functions in case of uniform convergence.
Power Series: Radius of convergence of its existence, Cauchy Hadamard theorem. Uniform and absolute convergence. Properties of sum function. Abet’s limit theorems. Uniqueness of P. S. having the same sum function, Exponential. Logarithm and trigonometric functions defined by power series and deduction of their salient properties.
Riemann integration: Upper sum and lower sum. Upper and lower integral. Refinement of partitions and associated results. Darboux theorem. Necessary and sufficient condition of integrability. Integrability of sum, product, quotient and modulus. Integral on the limit of a sum. Integrability monotone function, continuous function and piece wise continuous function. Primitive, properties of definite integral, Fundamental theorem of integral calculus First and second mean-value theorem of integral calculus (statements and applications only).
Improper Integrants: Tests of convergene : comparison and r-test (statement only). Absolute and non-absolute convergence-corresponding test (statement only). Working knowledge of Beta and Gamma functions and their interrelations.
Functions of two variable: Limit, continuity, partial derivatives. Functions on R2 differentiability, differential. Chain rule. Euler’s theorem, commutativity of partial derivatives statement of Schwarz and Young theorems.
Differential Equations
Significance of ordinary differential Equations: Geometrical and physical consideration. Formation of differential equation by elimination of arbitrary constants. Meaning of the solution of ordinary differential equation. Concepts of linear and non-linear differential equations.
Equations of first order and first degree: Statement of existence theorem. Separable, homogeneous and exact equations, condition of exactness, integrating factor. Equations reducible to first order linear equations. First order linear equations: Integrating factor. Equations reducible to first order linear equations. Equations of first order but not of first Degree: Clairaut’s equation, singular solution. Applications: Geometric applications, Orthogonal trajectories. Higher order linear equations with constant coefficients: Complementary function. Particulars integral, Symbolic operator. D. Method of variation of parameters. Euler Equations – reduction to an equation of constant coefficients.
ANALYTICAL GEOMETRY OF TWO AND THREE DIMENSIONS
TWO DIMENSIONS:
Transformations of rectangular Axes: Translation, Rotation and their combinations. Theory of Invariants.
General Equations of Second Degree in two variables: Reduction to canon.
Paris of straight lines: Condition that the general equation of second degree in two variable may represent two straight lines. Point of intersection of two intersection straight lines. Angle between two lines given by ax2 + 2hxy +by2 =0 Angle bisectors. Equation of two lines joining the origin to the points in which a line meets a conic.
Circle, parabola, ellipse and phyperbola : Equations of pair of tangents from an external point, chord of contact, Poles and Polars. Conjugate point and conjugate line.
Polar Equations: Polar equations of straight lines, circles and conic referred to a focus as pole, Equations of tangent, normal and chord of contact.
THREE DIMENSIONS:
Rectangular cartesion co-ordinate in space: half and octants concept of a geometric vector (directed line segment projection of a vector on co-ordinate axis. Inclination of a projection of a vector on co-ordinate axis. Inclination of a projection of a vector on co-ordinate axis. Inclination of a vector with an axix. Co-ordinates of a vector. Direction cosine of a vector. Distance between two points. Division of a directed segment in a given ratio.
Equation of plane: General form, intercept and Normal forms. The sides of a plane signed distance of a point from a plane. Equation of a plane passing through the intersection of two planes. Angle between intersection planes, Besectors of angels between two intersecting planes. Parallelism and perpendicularity of two planes.
Straight lines in space: Equation (symmetric and parametric form) Direction ratio and Direction cosines. Canonical equation of the line of intersection to two intersecting plane. Angle between two lines. Distance of a point from a line. Condition of coplanarity of two lines. Equations of skewlines. Shortest distance between two skew lines.
Sphere: General equation, circle, sphere-through the inter section of two-spheres. Radical Plane. Tangent, Normal.
General equation of 2nd degree in 3 variable. Reduction to canonical forms. Classification of quadrics.
VECTOR ALGEBRA & ANALYSIS:
Vector Algebra: Vector (directed line segment) Equality of two free vectors. Addition. Multiplication by a scalar. Position Vector: Point of division. Conditions of collinearity of 3 points and co planarity of 4 points. Rectangular components of a vector in two and three dimensions, product of two or more vectors: scalar and vector products, Scalar triple products and vector triple products. Products of four vectors.
Direct applications of vector algebra in (i) Geometrical, trigonometrically problems, (ii) Work done by a force. Moment of a force about a point, vectorial equations of straight lines and planes. Volume of trahedron. Shortest distance between two skew lines.
Vector Analysis: Vector differentiation with reference to a sector variable. Vector functions of one scalar variable. Derivative of a vector. Second derivative of a vector. Derivatives of sums and products. Velocity and Acceleration as derivative.
MECHANICS – I
Composition and Resolution of coplanar concurrent forces. Resolution of forces. Moments and Couples.
Reduction of a system of coplanar forces. Conditions of equilibrium of coplanar forces.
Fundamental ideas and principles of Dynamics. Laws of motion. Impulse and impulsive forces. Work, power and energy, principles of conservation of energy and momentum.
Motion in a straight line under variable acceleration. Motion under inverse square law. Composition of two S. H. M’s of nearly equal frequencies. Motion of a particle tied to one end of an elastic string. Rectilinear motion in a resisting medium. Damped forced oscillation. Motion under gravity where the resistance varies as some integral (nth) power of velocity. Terminal velocity.
Impact of elastic bodies. Newton’s experimental law of elastic impact. Loss of K. E. in a direct impact.
Expressions for velocity and acceleration of a particle moving on a plane in Cartesian and Polar co-ordinates. Motion of a particle moving in a plane in Cartesian and Polar co-ordinate.
Central forces and central orbits. Characteristics of central orbits.
Tangential and Normal accelerations. Circular motions.
Motion of a particle in a plane under different laws of resistance. Motion of a projectile in a resisting medium in which the resistance varies the velocity.
Laws of friction, cone of friction. To find the positions of equilibrium of a particle lying on a (i) rough plane curve, (ii) rough surface under the action of any given forces.
General formula for the determination of centre of gravity.
LINEAR PROGRAMMING PROBLEM (L.P.P.)
Definition of L.P.P. Formation of L.P.P. from daily life involving inequations. Graphical solution of L.P.P.
Basic solution and Basic Feasible solution (BFS) with reference to L.P.P. Matrix formulation of L.P.P. Degenerate and non-degenerate B.F.S. Hyperplane, convex set, Cone, Extreme points. Convex hull and convex polyhedron. Supporting and separating hyperplane. Simple results on convex sets like the collection of all feasible solutions of an L.P.P. constitutes a convex set.
The extreme points of the convex set of feasible solutions correspond to its
B. F.S. (no proof). The objective function has its optimal value at an extreme point of the convex polyhedron generated by the act of feasible solutions (no proof). Fundamental theorem (no proof). Reduction of a F.S. to a B.F.S.
Slack and Surplus variables. Standard form of L.P.P. theory of simplex method. Feasibility and optimality conditions.
The algorithm. Two phase method. Degeneracy in L.P.P. and its resolution.
Duality Theory: The dual of the dual to the Primal.
Relation between the objective values of dual and the primal problems. Relation between their optimal values. Complementary slackness. Duality and simplex method and their applications.
Transporation and Assignment problems, and that optimal solution.
MECHANICS – II
Laws of friction, cone of friction. To find the positions of equilibrium of a particle lying on a (a) rough plane curve, (ii) rough surface under the action of any given forces.
General formula for the determination of centre of gravity.
Astatic equilibrium, Astatic Centre. Positions of equilibrium of a Particle lying on a smooth plane curve under action of given forces.
Virutal work: Principle of virtural work for a single particle. Deduction of the conditions of equilibrium of a particle under coplanar forces from the principle of virtual work. The principle of virtual work for a rigid body. Forces which do not appear in the equation of virtual work. Forces which appear in the equation of virtual work. The principle of virtual work for any system of coplanar force acting on a rigid body.
Converse of principle of virtual work.
Forces in 3-dim: Moment of a force about a line. Axis of couple. Resultant of any number of couples acting on a rigid body. Reduction of a system of forces acting on a rigid body. Poinsot’s Central axix. Wrench, Pitch, Intensity and screw. Invariant and equation of the central axis of a given system of forces.
Motions under inverse square law in a plane. Escape velocity. Planetary motions and Keplar’s Laws. Artificial satellite Motion. Slightly disturbed orbit. Conservative field of force and principles of conservation of energy, Motion under rough curve (circle, parabola, ellipse, Cycliod) under gravity
RIGID DYNAMICS:
Moments and products of inertia. Theorem of parallel and perpendicular axes. Principles axes of inertia, momental ellipsoid Equimomental system. D’Alembert’s principle. Equation of Motion. Principles of moments. Principle of conservation of linear and angular momentum. Principles of energy.
Equation of Motion of a rigid body about a fixed axis.
Expression for K.E. and moment of momentum of a rigid body moving about a fixed axis. Compound pendulum.
Equation of Motion of a rigid body moving in 2-dim. Expression for K. E.and angular momentum about the origin of a rigid body moving in 2 dim. Motion of a solid revolution moving on a rough horizontal & inclined plane.. Conditions for pure rolling.
Impulsive action.
Generalised coordinates, momentum Lagrangian, Cyclic coordinates, Ronthian
A. MATHEMATICAL THEORY OF PROBABILITY
Random experiments. Simple and compound events. Event space. Classical and frequency definitions of probability and their drawbacks. Axioms of probability, Statistical regularity. Multiplication rule of probabilities. Bayes theorem. Independent events. Independent random experiments. Independent trials. Bernoulli trails and law. Multinominal law. Random variables, Probability distribution. Distribution function, descrete and continuous distributions. Bimominal, Poison, Uniform, normal distribution. Cauchy gamma distributions. Beta distribution of the first and of the second kind. Poison process. Transformation of random variables. Two-dim, prob. Distribution. Discrete and continuous distributions in two dimensions. Uniform distributions, and two-dimensional normal distribution. Conditional distributions. Transformation of random variables in two dimensions. Mathematical expectation. Mean, variance, moment, central moments. Measures of location, dispersion, skewness and Kurtosts. Median, Mode, quartiles, Moment-generating function characteristics function. Two dimensional expectation. Covariance. Co-relation Co-efficient. Joint characteristic function. Multiplication rule for expectations, conditional expectations, Regression curves, least square regression lines and parabolas. Chi square and distributions and their important properties, inequality Convergence in probability. Bermouli’s limit theorem. Law of large numbers. Poissons approximation to binomial distribution. Normal approximation to binomial distribution. Concept of asymptotically normal distributions. Statement of central limit theorem in the case of equal components and of limit theorem for characteristic functions and in applications. (Stress should be more on distributive function theory than on combinational problems. Different combinatorial problems should be avoided).
MATHEMATICAL STATISTICS:
Random samples. Distribution of the sample. Tables and graphical representations. Grouping of data. Sample characteristic and their computation. Sampling distribution of a statistic. Estimates of a population characteristic or parameter. Unbiased consistent estimates. Sample characteristics as estimates of the corresponding population
characteristics. Sampling distributions of the sample mean and variance. Exact sampling distributions for the normal populations.
Bivariate samples. Scatter diagram. Sample correlation coefficient. Least square regression lines and parabolas. Estimation of parameters. Method of maximum likelihood. Applictions to binomial. Normal populations. Confidence intervals. Such intervals for the parameters of the normal populations. Approximate confidence interval for the paratmer of a binomial population. Statistical hypothesis. Simple and composite hypothesis. Best critical region of a test. Neyman Pearson theorem and its applications to normal populations. Likelihood ratio testing and its applications to normal population.
NUMERICAL ANALYSIS
Computational Errors: Round-off errors, significant digits, errors in arithmetical operations, guard figures in calculations.
Interpolation: Polynomial Interpolation, remainder, Equally-spaced interpolating points-difference, difference table, propagation of errors; Newton’s forward and backward, Stirling and Bessel interpolation formulae, divided differences, divided difference, formula, confluent divided differences, inverse interpolation.
Numerical Differentiation: Error in numerical differentiation. Newton’s forward and backward and Lagrange’s numerical differentiation formula.
Numerical Integration: Degree of precision, open & closed formulae, composite rules. Newton-Cotes (closed-type) formula – Trapeezoidal, Simpson’s one third and Weddle’s rules, error formulae in terms of ordinates (proofs not necessary).
Numerical Solutions of Equations: Initial approximation by methods of tabulation and graph, methods of bisection, fixed point iteration with condition of convergence. Newton – Raphson & Regula-falsi methods, computable estimate of the error in each method.
Solution of ODE:
First Order First degree: By Euler, RK4 and Milne’s method.

Leave a Reply